Quote
http://ru.wikipedia.org/wiki/Производная_функции
Производной функции f(x) называют предел отношения приращения функции (Δy = f(x0 + Δx) − f(x0)) к приращению аргумента (Δx = x − x0) при изменении аргумента, стремящемся к нулю (Δx -> 0). Она обозначается как f'(x), dx/dy или x.(t) , тогда f'(x0) = lim (Δy/Δx). Задача вычисления производной известной функции является предметом изучения дифференциального исчисления, а обратная - интегрального.
f(x) -> f'(x) - дифференциальное исчисление
f'(x) -> f(x) - интегральное исчисление
Физический смысл производной - мгновенная скорость.
Геометрический смысл производной - угловой коэффициент касательной к графику функции - tg a.
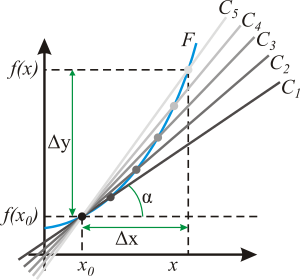
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Правила дифференцирования:
1) (u +- v)' = u' +- v'
2) (u * v)' = uv' + vu'
3) (u / v)' = (vu' - uv')/(v ^ 2)
4) (f o g)' = (f' o g)(x) o (g'(x))
const -> 0
x -> 1
x ^ n -> n * (x ^ (n - 1))
e ^ x -> e ^ x
sin x -> cos x
cos x -> -sin x
tg x -> 1 / (cos^2 x)
ctg x -> -1 / (sin^2 x)

